Claims that “the Universe will end sooner than expected” are false

Here in our Universe, a common refrain is that, “This, too, shall pass.” Our night sky is alight with a vast array of planets, stars, and galaxies: indicative of the complex structures that have formed through the relentless effects of gravitation over the past 13.8 billion years. Although quintillions of new stars will no doubt form within our observable Universe far into the future, our Universe is already past its prime in a significant number of ways. Most of the stars that will ever form have already formed, as star-formation only occurs at 3% of the rate it once possessed 11 billion years ago: at its peak. Many planets will be swallowed or ejected as their parent stars evolve, and all of the stars that now exist will someday become stellar corpses: white dwarfs (which will someday fade to black), neutron stars, and black holes.

However, it’s long been known — since as far back as 1974 — that black holes won’t persist forever. Instead, due to the intricacies of quantum field theories in curved spacetime, black holes will emit a very real form of energetic radiation: Hawking radiation, where the rate and temperature of the emitted radiation depends on the amount of curvature at and outside the black hole’s event horizon. For a black hole with the same mass as our Sun, it will decay after ~10⁶⁷ years: a very long time, but an importantly finite one.

Recently, in 2023, a team of authors published a paper suggesting that Hawking-like radiation isn’t just for black holes, and therefore, everything will eventually decay. In a follow-up paper, just recently published, they argue that this sets a new timescale for the lifetime, and the end, of the Universe. Unfortunately, a deeper examination reveals that the idea is fundamentally flawed. Here’s what everyone should know.

In Hawking’s most famous book, A Brief History of Time, he makes the analogy that space is filled with particle-antiparticle pairs and that one member can escape (carrying positive energy) while the other falls in (with negative energy), leading to black hole decay. This flawed analogy continues to confuse generations of physicists and laypersons alike.

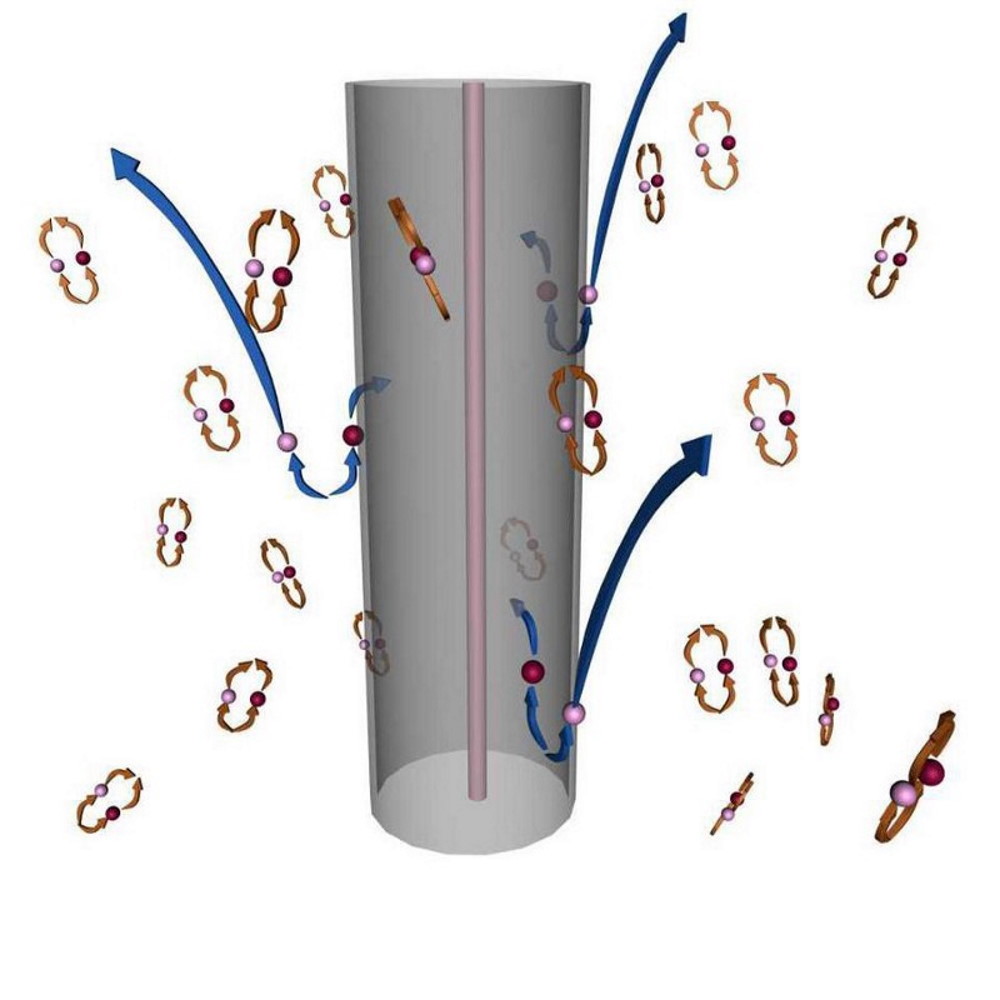
When most of us think about Hawking radiation, we hold a flawed and inaccurate picture of what’s occurring in our heads. That picture — put forth by Hawking himself in his immensely popular book A Brief History of Time — goes as follows.

• A black hole is a region of curved space with an event horizon separating the black hole’s interior (from which nothing can escape its gravitational pull) from the exterior (from which matter and radiation can escape).
• The Universe is filled with quantum fields, and those fields permeate all of space, including in regions with neither matter nor radiation present.
• Those quantum fields remain in the ground state in the absence of any real, physical effects, save for the quantum fluctuations (i.e., between energy and time) that occur.
• Those fluctuations can be visualized as particle-antiparticle pairs popping in-and-out of existence everywhere, including inside, outside, and right at the boundary of the black hole’s event horizon.
• When fluctuations occur inside or outside, they remain there and go “back to zero,” but fluctuations at the horizon can have one member of the pair “fall in” and the other member “escape,” allowing for the emission of real radiation: Hawking radiation.
• Finally, the escaping radiation carries real energy, and since energy is conserved, it must come from somewhere: from the mass of the black hole itself, via Einstein’s E = mc².

If you’ve ever heard an explanation for Hawking radiation, it’s very likely that it went something like the above line-of-thinking I just recounted, as it paraphrases Hawking very accurately.

The most common, and incorrect, explanation for how Hawking radiation arises is an analogy with particle-antiparticle pairs. If one member with negative energy falls into the black hole’s event horizon, while the other member with positive energy escapes, the black hole loses mass and outgoing radiation departs the black hole. This explanation has misinformed generations of physicists and came from Hawking himself. One of the errors inherent to this explanation is the notion that all of the Hawking radiation arises from the event horizon itself: it does not.

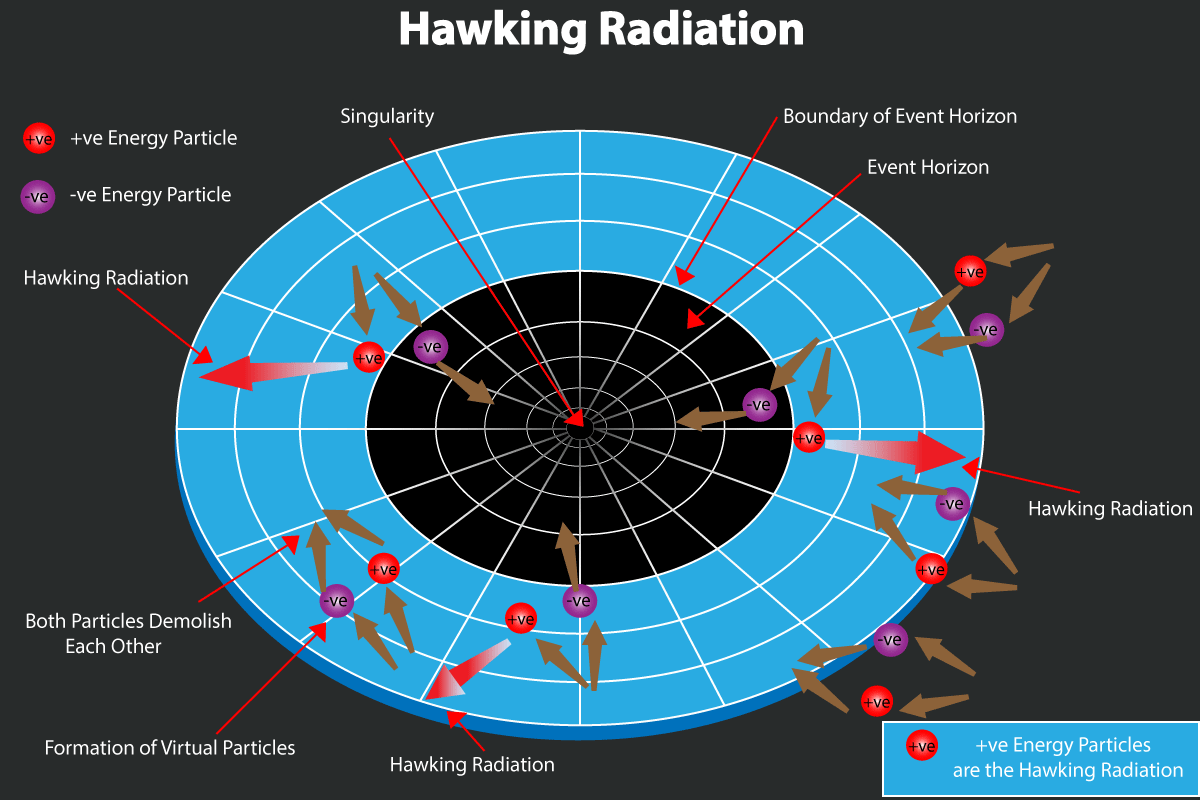
But only the first three steps of that explanation are accurate in any way. Hawking radiation doesn’t arise because of any particle-antiparticle fluctuations that occur; that’s merely a calculational tool we use in quantum field theory to help us visualize (and calculate quantitative estimates for) how these quantum fields behave. What actually happens is instead more subtle.

• In all regions where space is curved, including outside, inside, and at the event horizon, the quantum vacuum possesses different properties for its lowest-energy (or ground) state: the state that it will reside in even in the absence of all forms of matter or radiation.
• Because of Einstein’s equivalence principle, we can think about spacetime curvature as being equivalent to any other form of acceleration; gravitational acceleration is just another example of mechanical acceleration.
• Therefore, if we look at the behavior of quantum fields across different regions of space — especially nearer to the event horizon, where curvature is more severe, and farther from the event horizon, where curvature is less significant — we’ll find that there’s a difference in the quantum vacuum’s ground state between those regions.
• It is that difference that induces the emission of real radiation: not in the form of charged particles or their antiparticles, but in the form of photons: what you’d expect to be produced as blackbody radiation for any object heated up to a specific temperature, in this case, the Hawking temperature.

In other words, it isn’t the production of quantum “pairs of particles” that causes the existence of Hawking radiation, but rather the difference in the quantum vacuum between regions closer to and farther from the event horizon.

Visualization of a quantum field theory calculation showing virtual particles in the quantum vacuum. (Specifically, for the strong interactions.) Even in empty space, this vacuum energy is non-zero. If there are additional particles or fields beyond what the Standard Model predicts, they will affect the quantum vacuum and will change the properties of many quantities away from their Standard Model predictions. However, the QCD contribution cannot be calculated perturbatively, the way electromagnetism can.

It’s not true that particle-antiparticle pairs are always popping in-and-out of existence, but this visualization remains a common one. What is true is that quantum fields do indeed carry energy, that energy can be converted into real, massive particles (if there’s enough of it) via the Schwinger effect, and that black holes should indeed produce a real form of radiation via Hawking radiation. It’s also true that accelerated observers even in flat, empty space will experience a uniform bath of radiation as well, in the form of Unruh radiation, which should appear in our accelerating Universe in the far future at extremely low (~10^-30 K) temperatures, owing to the existence of dark energy.

However, there’s an important caveat to Hawking radiation (for black holes) and for Unruh radiation (for accelerated observers): they require the existence of some type of “horizon” in order to be physically real. A horizon is defined as the boundary between a region where slower-than-light-speed phenomena can physically affect you and where only faster-than-light-speed phenomena could ever physically reach you. For a black hole, that’s the event horizon; for an accelerated observer (or for dark energy in our accelerating Universe), that’s a cosmological horizon. The energy needs a source, or a place where it can come from, and for quantum field theories in curved spacetime, that’s the big idea: it must come from some sort of horizon.

The event horizon of a black hole is a spherical or spheroidal region from which nothing, not even light, can escape. But outside the event horizon, the black hole is predicted to emit radiation. Hawking’s 1974 work was the first to demonstrate this, but that work has also led to paradoxes (i.e., the black hole information paradox) that have yet to be resolved.

Now, there are some interesting points to note when we think about Hawking radiation arising from a black hole.

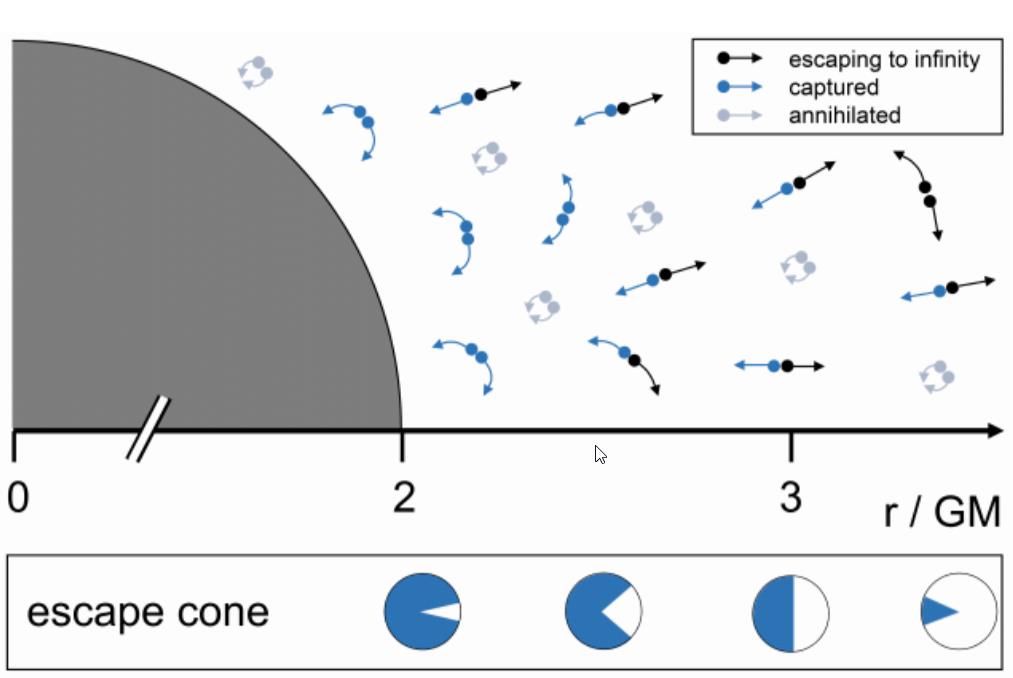
You might be tempted to think, “Oh, okay, all of the Hawking radiation that exists comes from the black hole’s event horizon, or the boundary between faster-than-light and slower-than-light entities can escape.” But that’s not true! We can calculate the energy density of the Hawking radiation that arises all throughout the space outside of the black hole’s event horizon, and it does not equal the expected energy density if you had all of the radiation originate at the horizon. It’s as though the horizon determines whether this type of radiation (e.g., Hawking radiation) is possible, but it doesn’t provide a point-of-origin for all of the radiation itself.

You might also think that more massive black holes would have larger and more massive event horizons, and therefore they’d radiate more energetically, but it turns out that the opposite of that is true! The lowest-mass black holes have the smallest event horizons, but the largest amounts of spatial curvature at the location of the event horizon, implying that as black holes radiate and lose mass, they evaporate faster and faster as time goes on.

And finally, the spacetime curvature far away from a mass — whether it’s a star, white dwarf, neutron star, or black hole — is the same regardless of the density or volume of the mass. As long as 100% of the mass is “enclosed” within the volume you’re considering, the spatial curvature at your location remains unchanged even as you vary the density or volume of your object.

Although the amount that spacetime is curved and distorted depends on how dense the object in question is when you’re close to the object’s edge, the size and volume that the object occupies is unimportant far away from the mass itself. For a black hole, neutron star, white dwarf, or a star like our Sun, the spatial curvature is identical at sufficiently large radii. However, close to the event horizon of a black hole, more severe curvatures are achieved than anywhere else. Far away from all of these sources, spacetime is asymptotically flat, but neither perfectly flat nor truly empty.

The original idea of the first (2023) paper by Michael Wondrak, Walter van Suijlekom, and Heino Falcke was actually straightforward, and leveraged this very line of thinking. The authors reasoned that spatial curvature doesn’t care about how dense your object is or whether the event horizon is present or absent. Since it’s just the difference in curvature, and particularly the difference in curvature between different regions of space, that induces differences in the quantum vacuum, then this type of radiation should exist anywhere that we have changing regions of spatial curvature. And since it’s mass that causes spatial curvature most commonly (in our experience), then any mass can induce a difference in the quantum vacuum from place-to-place.

If the quantum vacuum is different, then we should be able to produce Hawking radiation between those regions: propagating outward from the region of greatest curvature (i.e., where the mass is located). The authors then go on to perform an approximate calculation, where they model the production of radiation by a simple scalar field, and where they use the (knowingly flawed) particle-antiparticle pair production analogy to perform their estimates. What they found was simple and straightforward: if you take this analogy seriously, you wind up getting comparable answers to what we’d predict for the production of Hawking radiation near a black hole, but for any mass at all.

The event horizon of a black hole has been considered an important factor in the generation of Hawking radiation around black holes in many previous studies, but a new one from 2023 suggests that this radiation can still be generated outside of an event horizon even if the “horizon” itself does nothing more than forbid light from escaping from within it. This picture is non-rigorous as formulated, however, and others have disputed these claims.

I wrote about this back in 2023, as I found the idea intriguing. Then, in late 2024, they released a follow-up paper that prompted an Ask Ethan column, and I wrote about it again, noting that this would imply a finite lifetime for everything that existed within our Universe. This includes:

• individual protons, which would have a lifetime of around ~10⁶⁷ years, similar to a solar mass black hole,
• white dwarfs, which should decay away after around ~10⁸⁰ years,
• low-mass planetary bodies, like Earth’s moon, which should live for only around ~10⁹⁰ years,
• the largest supermassive black holes, which might live for around ~10¹⁰⁵ years,
• and even big, fluffy, diffuse dark matter halos, which would require even longer timescales of between ~10¹²⁰ and ~10¹⁴⁰ years.

This would imply some serious cosmic violations. For example, for the proton to decay, we’d have to violate baryon number conservation: something that should be theoretically possible (after all, we have a baryon-over-antibaryon asymmetry in our Universe today), but for which no direct experimental evidence exists. For white dwarfs or planetary bodies to decay, we’d have to have some way to extract energy from a maximally gravitationally bound system, otherwise the demands of E = mc² imply that some type of conservation law violation would need to exist. The authors do not come up with an explanation for this; they simply suggest that this could occur.

The evaporation timescales (y-axis) versus the mass density of the object in question (x-axis), with various notable points shown corresponding to a variety of quantum and cosmic entities. This calculation was based off of an estimation for how such objects would decay in a non-rigorous fashion; whether these decays would actually occur has not been adequately established by the study’s authors.

But is that true? Can this process occur, and more importantly, can it occur in the absence of a horizon: which only black holes (for an event horizon) and the expanding Universe, overall (for a cosmological horizon) actually possess?

When I wrote my original articles, I incorrectly stated that this had yet to be decided. This was due to a lack of my own personal knowledge; this is something that was actually known within the field of quantum gravity research (i.e., at the intersection of quantum field theory and the curved spacetime backgrounds predicted by general relativity) as far back as 1975!

Back in 1975, scientists Abhay Ashtekar and Anne Magnon were considering how to formulate a quantum field theory in spacetimes of various types of curvature. Although the paper itself is very technical, one important consideration that comes up is the difference between a spacetime with a stable quantum vacuum, which is one where we have what’s known as a time-like Killing field (i.e., where the Universe has a time-translation symmetry, which is equivalent to the statement that energy is conserved), and one where the Killing field is allowed to be space-like in certain regions, which means that certain vital energy conditions are no longer obeyed, and many resulting pathologies arise.

In the vicinity of a black hole, space flows like either a moving walkway or a waterfall, depending on how you want to visualize it. At the event horizon, even if you ran (or swam) at the speed of light, there would be no overcoming the flow of spacetime, which drags you into the singularity at the center. Outside the event horizon, though, other forces (like electromagnetism) can frequently overcome the pull of gravity, causing even infalling matter to escape. Rotating black holes possess ring-like, not point-like, singularities.

Now, this is where we have to be careful. You might ask, “Are there any situations where these conditions arise that correspond to something actually present within our Universe?”

And the answer is yes. The Universe has a time-like Killing field wherever it has a point mass, including for the types of point masses considered in the calculations of Wondrak, van Suijlekom, and Falcke: a massive spin-zero scalar particle. The lone exceptions to space possessing a time-like Killing field occur where:

• either we have a cosmological horizon, as in the instance of the expanding Universe,
• or we have an event horizon, such as around a Schwarzshild (non-rotating) or a Kerr (rotating) black hole.

In other words, the presence or absence of a horizon, either a cosmological horizon or an event horizon, is in fact the key ingredient that’s necessary for this type of radiation, either Unruh or Hawking radiation, to physically exist. As others have pointed out, the key sentence from the Ashtekar and Magnon paper explicitly states:

“Thus, if the underlying space-time admits a everywhere time-like Killing field, the vacuum state is indeed stable and phenomena such as the spontaneous creation of particles do not occur.”

Black holes formed of different materials should have different information encoded on their event horizons, and it is not understood if or how that information is then encoded in the outgoing Hawking radiation. Recent work has suggested that even horizonless objects may emit Hawking radiation, but that calculation is incomplete and based on flawed assumptions. A horizon is required to violate time-like behavior for the spacetime’s Killing field, and in the absence of a horizon, no decay will occur.

So that’s it: that’s the answer. The gravitational field of a static object can only create particle-antiparticle pairs if that static object possesses a horizon, or a place where the Killing field no longer exhibits time-like behavior everywhere. If such a location does not exist for an otherwise static object, that object cannot radiate via the Hawking (or Unruh) mechanism, and therefore it will not have a finite lifetime or spontaneously decay to the full extent of our knowledge. This was pointed out in the peer-reviewed literature as a follow up to Wondrak, van Suijlekom, and Falcke’s paper in a comment in November of 2024 and in an independent paper at precisely the same time.

When we consider these aspects of what’s already known about reality, we arrive at the answer. Only objects with horizons, either event horizons or cosmological horizons, can radiate and decay the way black holes can. Other massive objects, from protons to stars to stellar and planetary corpses to dark matter halos, will remain stable against decay via Hawking radiation infinitely far into the future. (Although it is still plausible that other decays, unknown to us at present, could still occur.) As fascinating as the idea is that the Universe, and everything in it, will someday succumb to Hawking radiation, the physics of general relativity and quantum field theory in curved spacetime says otherwise. Until we have knowledge that takes us beyond this framework, we cannot validate the idea that our Universe is unstable in such a fashion.